 |
 |
 |
 |
 |
 |
 |
 |
|
 |
|
 |
|
| 第七节 辐射度方法 | ||||
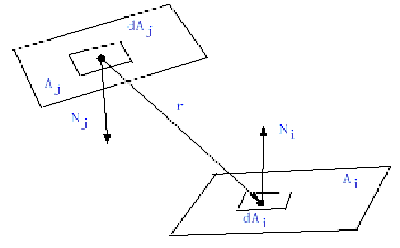 图8.11 形状因子的计算中所涉及的各量的图示 当环境中有遮挡关系存在时，应在上面的积分式中加入一个系数  ，它的取值为0或者1，取1时，表示第i个面的位置可以看见第j个面的相应位置，取0时，则不可见。
为了方便的计算形状因子，我们可以采用hemicube方法.即在受光的面片中心周围构造一个半正方体。使受光面中心成为新坐标系中心，面片的法向方向为z轴方向。把此半正方体分成一些网格，每个网格对应一个形状因子。要计算一个面片的形状因子，则可把该面片投影到半正方体上。投影所覆盖网格的小形状因子之和，就是面片的形状因子。 如果若干个面片投影到半立方体的同一个网格上，则可以通过比较这些面到受光面片的距离，来确定哪一个面片离受光面片更近。 现在来看面片的形状因子的计算，因为 
其中，△Fq是第q个具有投影的小网格的形状因子。现在的任务是如何来求△Fq。 对于顶面上的网格，其小形状因子值为： 
|
||||
 第一节
漫反射及具体光源的照明第二节
多边形网的明暗处理第三节
阴 影第四节
纹 理第五节
整体光照明模型第六节
光线跟踪第七节
辐射度方法第八节
色彩模型 |