| 第七节 辐射度方法 | ||||
| 公式实际上是含有N个未知数 辐射度方法的含义是:离开一个特定的面的光能等于它所发出的光和反射光能之和。当然,反射光等于离开其它各个面的光亮度乘以形状因子,再乘以该面的反射率。 把辐射度公式写成矩阵乘积的形式为: 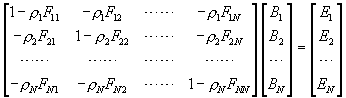
对于平面或凸面, 在不存在遮挡关系的环境中,在二个微分面之间,从一个微分面元到另一个微分面元的形状因子为: 
它表示从 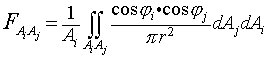
|
||||


|
||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||
| 上一页 | 下一页 | ||||||||||||||||||||||||||||||