第四节 0-1型整数规划     (1) (2) (3)
    今设集装箱有车运和船运两种方式，（3）式是车运时的重量限制条件。如用船运时关于重量的限制条件为 2X1+5x2≤20 试确定集装箱托运甲、乙货物的数量及运输方式，使总利润最大。
    为了建立问题的模型，除了设甲、乙货物托运的件数分别为X1,X2外，还要把运输方式表示出来。由于只有两种运输方式，所以可设
        
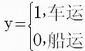
    在约束条件中，两种不同运输方式对应的重量约束条件是相互排斥的，所以不能简单地将它们都写到约束中。利用y这个0—1变量可以将上述两个重量约束改写成：
    2X1+5X2≤13+（1-y）M ⑸
    2X1+5X2≤20+yM ⑹
    其中M是相当大正数，显然当y=1时，⑸式就是车运的重量限制条件，而⑹式自然成立，因而是多余的；当y=0时，⑹式就是船运的重量限制条件，而⑸式成为多余的。经过这样处理后，问题的数学模型可以写成如下形式：
        
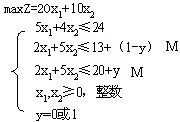
    类似地，如果有m个相互排斥的约束条件：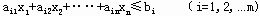
    为了保证这m个条件只有一个起作用，可以引入m个0—1变量 yi（i=1,2,…m)和充分大正常数M，将这个约束条件改写成：
    
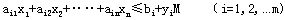
    显然，这些yi中只能有一个取0值，因而这m个约束只能有一个起作用，而其余都是多余的。