第四节 0-1型整数规划     (1) (2) (3)
    4.2 0—1 型整数规划的解法
    对于0—1型整数规划的求解问题，由于每个变量只取0、1两个值，人们自然会想到用穷举法来求解，即排出变量取值为0或1的每一种组合（共2n个点) ，验证它们是否满足约束条件，再算出每个可行解的目标函数值，比较各函数值以求得最优解。显然当n较大时，计算量是相当大的。（如210=1024）因此，常设计一些方法，只检查变量取值组合的一部分，就能求得问题的最优解。这一类方法称为隐枚举法。
    为了便于应用隐枚举法，当目标函数要求极大值时，可先将 0—1型整数规划中变量的顺序重新排列，使在目标函数中的系数呈递增（不减）的,并且按二进制数码从小到大的顺序排列每一组解，即按（00…00）、（00…01）、（00…10）…（11…11） 的顺序排列。这样，可使最优解容易比较早地发现，使得计算简化。
    下面举例说明如何运用隐枚举法求解0—1 型整数规划。
    例5 求解
        
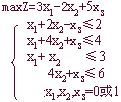
    解：调整X1,X2的顺序，使目标函数中变量的系数呈递增（不减）的顺序,则问题变为：
        
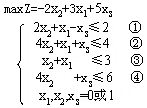
    按二进制数码从小到大的顺序排列并检查各个解，先计算解的目标值，若目标值小于目前可行解最好的目标值，则不必检查是否满足约束条件，当所有解被检查完毕，就可判断出最优解。计算结果可列表表示，见下表。
        
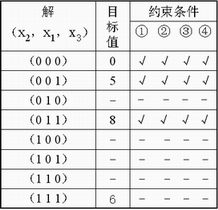
    最终得到最优解：X1=1，X2=0，X3=1，最优值：Z=8