第五节
指派问题 (1)
(2) (3)
根据指派问题的特殊结构,我们有更为简便的方法。这就是下面将介绍的匈牙利法,这个方法是由匈牙利数学家康尼格(D.Konig)给出的。
匈牙利算法是以指派问题最优解的性质为根据的。
指派问题最优解性质:如果将指派问题的效率矩阵的每一行(列)的各个元素都减去该行(列)的最小元素,得到一新的矩阵
C′,则以C′为效率矩阵的指派问题的最优解与原问题的最优解相同。
证明:设C的第i行元素都减去该行最小元素ai,第j列元素都减去该列最小元素bj
,则新矩阵C′第i行第j列的元素为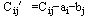 ,以新矩阵C′为效率矩阵的指派问题的目标函数为 ,以新矩阵C′为效率矩阵的指派问题的目标函数为
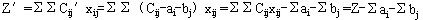
可见新问题的最优解与原问题的最优解相同,只是目标值相差一个常数。证毕。
利用这个性质,可以使原效率矩阵变换为含有多个0元素的新效率矩阵,而最优解不变。在新的效率矩阵中如果能找到n个不同行且不同列的0元素,则可以令它们对应的Xij等于1,其它Xij等于0,显然,该解一定是最优解。这就是匈牙利算法的基本思想。
具体步骤如下:
第一步 变换效率矩阵,使各行各列都出现 0 元素。
1°效率矩阵每行元素都减去该行最小元素;
2°效率矩阵每列元素都减去该列最小元素。
第二步 圈出不同行且不同列的 0 元素,进行试指派。
1°(行搜索)给只有一个0 元素的行中的0 画圈,记作“◎”,并划去与其同列的其余0元素;
2°(列搜索)给只有一个0 元素的列中的0 画圈,记作“◎”,并划去与其同行的其余0元素;
3°反复进行1°、2°,直至所有0元素都有标记为止。
4°若行(列)的0元素均多于一个,则在0元素最少的行(列)中选定一个0元素,标“◎”,并划去与其同行同列的其余0元素。
5°若不同行且不同列的 “◎”已达n个,则令它们对应的 Xij=1,其余 Xij=0,已得最优解,计算停,否则转第三步。
第三步 用最少直线覆盖效率矩阵中的0元素。
1°对没有“◎”的行打“√”;
2°对打“√”行中的0元素所在列打“√”;
3°对打“√”列中“◎”所在行打“√”;
4°反复进行2°、 3°,直至打不出新 “√”为止。
5°对没 打“√”的行画横线,对打“√”列画竖线,则效率矩阵中所有0元素被这些直线所覆盖。
第四步 调整效率矩阵,使出现新的0元素。
1°找出未被划去元素中的最小元素,以其作为调整量θ;
2°矩阵中打“√”行各元素都减去θ,打“√”列各元素都加θ(以保证原来的0元素不变),然后去掉所有标记,转第二步。 |

