第五节 指派问题     (1) (2) (3)
    下面用上述算法求解例6。
    解：先变换效率矩阵，然后圈出不同行不同列的0元素，结果如下：
        
    由于不同行不同列的0元素仅有3个，所以要继续第三步及第四步。
        
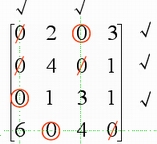
    调整量θ=1，调整效率矩阵使之出现更多0元素。
    而后，再重新圈出不同行且不同列的 0 元素，进行再指派。结果如下：
        
    由于◎的个数已达n=4个，所以令◎所对应的 Xij=1，其余 Xij=0，已得最优解。即最优指派方案为：张—C；王—A；李—D；赵—B。所需最少总时间为：5+6+9+3=23。注意，本例的最优方案不唯一，张—A；王—C；李—B；赵—D也是最优方案。
    以上讨论仅限于极小化问题，对于极大化问题，不能按minZ′=ΣΣ(-Cij)Xij求解，因为匈牙利法要求效率矩阵的元素Cij≥0，这时可取M=max｛Cij｝,令bij=M-Cij,以B=（bij）n×n为效率矩阵求解。
    ∵ΣΣ（M-Cij）Xij=nM-ΣΣCij Xij
    ∴当ΣΣ（M-Cij）Xij取最小时，ΣΣCij Xij便为最大。
    另外，如果任务数与人数不相等，可以象不平衡运输问题一样，虚设一项任务或人，并且令相应的或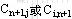等于0，（i,j=1,2…n）然后用匈牙利法求解。