第六节
中国邮递员问题 (1)
(2) (3)
6.1 欧拉图
欧拉图问题起源与著名的哥尼斯堡七桥问题,它的实质是如何判断一个连通图能否一笔不重复地画出。这个问题是由大数学家欧拉解决的,所以称为欧拉图问题。
定义:给一个连通多重图G,若存在一条链(圈)过每边一次且仅一次,则称这条链(圈)为欧拉链(圈)。
定义:一个图如果存在欧拉圈,则称之为欧拉图。
显然,一个图若能一笔不重复地画出,则这个图就是欧拉图或含有欧拉链。
定理:连通多重图G是欧拉图,当且仅当图中无奇点。
这个定理的结论是显然的,因为欧拉图从某一点出发又回到原来的出发点,这就要求与每个顶点相关联的边数应是偶数,从而才能保证从一条边进入该点,从与该点相关联的另一条边出去。
推论:连通多重图G有欧拉链,当且仅当G恰有两个奇点。
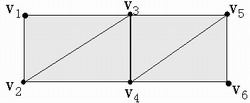
上面的定理和推论提供了识别一个图能否一笔不重复画出的简单方法。如下图,有两个奇点,所以能一笔不重复地画出,从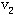 奇点开始一笔画到奇点 奇点开始一笔画到奇点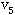 。 。
|

