第一节 图与网络的基本概念       (1) (2)
    在实际生活中，人们为了反映一些对象及它们之间的关系，常常画出各种各样的示意图。例如下图表示a城到g城的交通图，图中的b、c、d、e、f 表示中途经由的城市，二城之间的联线表示二城间的公路。
        
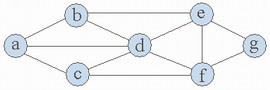
    通常，人们用点代表研究的对象（如城市、球队等等），用点之间的连线表示两个对象之间的特定关系（如两城之间的公路或两个球队之间的比赛等）。
    一般，称由一些点和一些边组成的集合为图，记作G=（V，E）， 其中V是点的集合，E是边的集合。图G中所含的点的个数，一般记作p(G)；所含的边的个数，一般记作q(G)。
    图论中的图与一般的投影图是完全不同的概念。图论中的图是反映对象之间的关系，在一般情况下，图中点的相对位置如何，点之间连线的长短曲直，对于反映对象之间的关系并不重要。
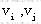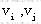    一条联结点∈V的边记作e =[]，称 为e 的端点，称e 为 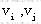的关联边。在图中具有同一条关联边的点称为相邻点，具有公共端点的边称为相邻边。
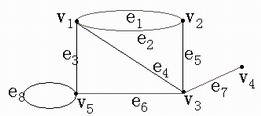
    某个边的两个端点相同，则称该边为环（如图7-4中的e8）。若两点之间有多于一条边相关联，则称这些边为多重边（如图7-4中的e1，e2）。一个无环、无多重边的图称为简单图，一个无环、但有多重边的图称为多重图。点v 的关联边个数称为点v 的次，记作d(v）。如图7-4中d(V1）=4，d(V2）=3，d(V3）=4，d(V4）=1，d(V5）=4。
    称次为1的点为悬挂点，悬挂点所关联的边为悬挂边。下图中的V4为悬挂点，e7为悬挂边。
        
    定理1 图G=（V，E）中，所有点的次数之和等于边数的两倍。 这是显然的，因为在计算各点的次时，每条边都被用了两次。 次为奇数的点，称为奇点；次为偶数的点，称为偶点。
    定理2 任一图中，奇点的个数必为偶数。