第一节
图与网络的基本概念 (1)
(2)
证明:设V1和V2分别是图中奇点和偶点的集合,q 为G中边的个数,则
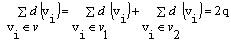
因为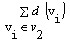 是偶数,所以
是偶数,所以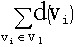 也是偶数,从而中奇点个数必为偶数个。
也是偶数,从而中奇点个数必为偶数个。
链:图G中,点边交错序列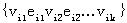 ,如果满足 ,如果满足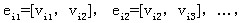 则称这个点边交错序列为 则称这个点边交错序列为
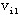 到 到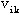 的链。
的链。
圈: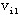 = =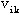 的链称为圈。
的链称为圈。
连通图:图G中,若任何两点之间,至少有一条链,则称G为连通图,否则称为不连通图。
子图:设有图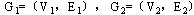 ,如果 ,如果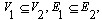
则称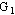 是 是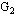 的子图。如果 的子图。如果
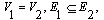 则称 则称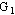 是 是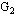 的真子图;如果 的真子图;如果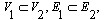 则称
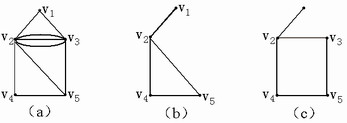
则称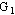 是 是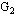 的部分图。例如下图中,(b)是(a)的真子图,(c)是(a)的部分图。 的部分图。例如下图中,(b)是(a)的真子图,(c)是(a)的部分图。
在很多实际问题中,事物之间的联系是有方向的。例如交通图中两点之间的单行路。我们把这种带有方向的线叫作弧,记作a=(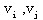 ),其中 ),其中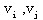 分别是弧a的起点和终点。称由一些点和弧组成的集合为有向图,记作D=(V,A),A是弧集。如下图是有向图。 分别是弧a的起点和终点。称由一些点和弧组成的集合为有向图,记作D=(V,A),A是弧集。如下图是有向图。
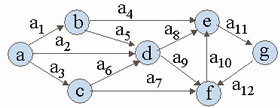
路:有向图D=(V,A)中,点弧交错序列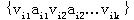 ,如果满足 ,如果满足 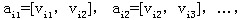 则称这个点弧交错序列为 则称这个点弧交错序列为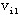 到 到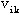 的路。 的路。
回路: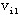 = =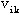 的路称为回路。如上图中
的路称为回路。如上图中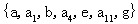 是a到g的一条路; 是a到g的一条路;
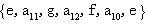 是一条回路。 是一条回路。
|

