第四节
网络最大流问题 (1)
(2)
许多系统都包含了流量问题。例如公路系统中有车辆流,控制系统有信息流,供水系统有水流等等。
现在考虑这样一个问题:某物资有m个生产基地A1,A2,…,Am要通过铁路运到n个销地B1,B2,…,Bn去。把铁路网上的车站看作是顶点,两个车站间的铁路线看作是弧。可以认为在某条铁路线上可运送的物资数量是有限的,我们把某条线路上的允许最大运送量称为容量。这时要考虑如何安排运输方案,使得由产地运到销地的物资总量达到最大。这就是在这个运输网中,求最大流问题。
4.1 网络最大流概念
容量网络:在有向图D=(V,A),指定一个点为发点,记作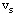 ,指定另一个点为收点,记作
,指定另一个点为收点,记作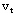 ,其余点叫作中间点。对于A的每条弧( ,其余点叫作中间点。对于A的每条弧( ,
,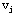 ),都对应一个权数
),都对应一个权数 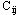 ≥0,称为弧( ≥0,称为弧( ,
,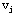 )的容量,将这样的赋权有向图叫作一个容量网络,记作D=(V,A,C)。
)的容量,将这样的赋权有向图叫作一个容量网络,记作D=(V,A,C)。
如果在一个网络中,有多个发点或收点,则我们可以将其变为只有一个发点和收点的网络。这只需增加一个新的总发点和一个新的总收点。从总发点到各个发点分别连接一条容量为+∞的弧,从各个收点到总收点分别连接一条容量为+∞的弧。这样就可将问题变为单发点和单收点的网络流问题。所以,以后我们只讨论一个发点和一个收点的网络流问题。
在网络中,将通过弧( ,
,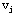 )的运量记作,并称之为弧(
)的运量记作,并称之为弧( ,
,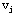 )上的流量。
)上的流量。
可行流:对于容量网络D=(V,A,C),每条弧( ,
,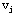 )都给定一个流量
)都给定一个流量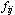 ,当{
,当{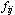 }满足下列条件时,称为可行流。 }满足下列条件时,称为可行流。
1°容量限制:对每条弧( ,
,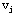 )∈A,有0≤ )∈A,有0≤
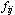 ≤ ≤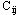 。 。
2°平衡条件:对于中间点 ∈V,流入量等于流出量,即 ∑
∈V,流入量等于流出量,即 ∑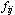 =∑ =∑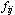 。 。
对于发点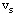 和收点 和收点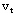 ,则有
发出总量等于 ,则有
发出总量等于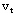 收到总量,即 收到总量,即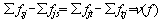 ,称v(f)为可行流{
,称v(f)为可行流{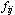 }的流量。 }的流量。
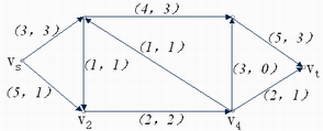
如下图中,弧旁的数字分别为(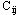 ,
,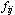 ),可以验证给出的流是可行流。 ),可以验证给出的流是可行流。
对于任何网络总是存在可行流的,比如令所有弧上的流都等于0,就可以得到一个可行流,其流量v(f)
=0。
最大流:使v(f)达到最大的可行流称为最大流。
|

