第三节
最短路问题 (1)
(2) (3)
在实践中常遇到的一类网络问题是最短路问题。给定一个有向赋权图D=(V,A),对每一个弧a
=(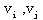 ),相应有权 ),相应有权
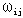 ≥0,指定D中的 ≥0,指定D中的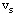 为发点, 为发点,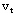 为终点。最短路问题就是要在所有 为终点。最短路问题就是要在所有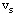 到 到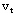 的路中,求出一条总权数最小的路。这里权数可以是距离,也可以是时间,或者是费用等等。 的路中,求出一条总权数最小的路。这里权数可以是距离,也可以是时间,或者是费用等等。
最短路问题是最重要的优化问题之一,它不仅可以直接应用于解决生产实际的许多问题,如管道铺设、线路安排、厂区布局、设备更新等等,而且经常被作为一个基本工具,用于解决其它优化问题。
3.1 狄克斯拉(Dijkstra)算法
最短路问题可以化为线性规划问题求解,也可以用动态规划方法求解,这里介绍一种有效算法—狄克斯拉(Dijkstra)算法,这一算法是1959年首次被提出来的。该算法适用于每条弧的权数
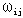 ≥0情形。算法的基本思路:从发点 ≥0情形。算法的基本思路:从发点
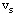 出发,有一个假想的流沿网络一切可能的方向等速前进,遇到新节点后,再继续沿一切可能的方向继续前进,则最先到达终点 出发,有一个假想的流沿网络一切可能的方向等速前进,遇到新节点后,再继续沿一切可能的方向继续前进,则最先到达终点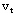 的流所走过的路径一定是最短的。为了实现这一想法,对假想流依次到达的点,依次给予p标号,表示
的流所走过的路径一定是最短的。为了实现这一想法,对假想流依次到达的点,依次给予p标号,表示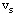 到这些点的最短距离。对于假想流尚未到达的点给予T标号,表示 到这些点的最短距离。对于假想流尚未到达的点给予T标号,表示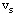 到这些点的最短距离的估计值。具体作法如下: 到这些点的最短距离的估计值。具体作法如下:
1°标p(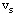 )=0,其余点标T( )=0,其余点标T( )=+∞; )=+∞;
2°由刚刚获得p标号的  点出发,改善它的相邻点 点出发,改善它的相邻点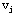 的T标号,即 的T标号,即
新的T(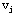 )=min{老的T( )=min{老的T(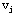 ),p( ),p( )+ )+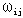 }
}
若T(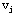 )=
p( )=
p( )+ )+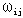 ,则记k(
,则记k(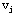 )= )= (前点标记); (前点标记);
3°找出具有最小T标号的点,将其标号改为p标号。若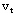 已获得p标号,则已找到最短路,由k( 已获得p标号,则已找到最短路,由k(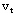 )反向追踪,就可找出 )反向追踪,就可找出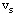 到 到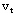 的最短路径,p( 的最短路径,p(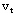 )就是 )就是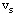 到 到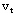 的最短距离。否则,转2°。 的最短距离。否则,转2°。
|

