第三节
最短路问题 (1)
(2) (3)
最短路问题不仅可以求解交通图中两点之间的最短距离,实际中很多问题也可变为最短路问题加以求解。例如设备更新问题,厂区合理布局问题等。兹举一例:
例3(设备更新问题)某企业使用一台设备,在每年年底,企业都要决策下年度是购买一台新设备呢?还是继续使用这台设备。若购买新的,就要支付一笔购置费;如果使用旧设备,只要支付维修费,而维修费随着设备的使用年限延长而增加。现根据以往统计资料已经估算出设备在各年初的价格和不同使用年限的修理费用,分别如表7-1、表7-2所示。
试确定一个五年内的设备更新计划,使五年内总支出最小。
3.2 图上标示法
下面我们结合例3介绍求解最短路问题的图上标示法,它比狄克斯拉算法更简洁。
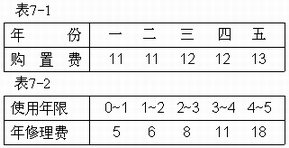
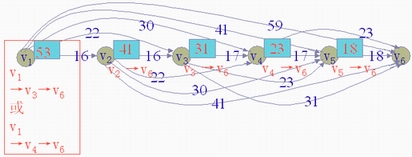
解:先根据表7-1、表7-2的数据画出设备更新费用网络图,如图7-14所示。图中点 表示第i年开始,弧( 表示第i年开始,弧( ,
,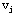 )表示设备第i
年初使用到第j 年初,弧( )表示设备第i
年初使用到第j 年初,弧( ,
,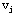 )上的权数表示该期间设备所需的费用。这样,求五年内设备最优更新方案便转化为求 )上的权数表示该期间设备所需的费用。这样,求五年内设备最优更新方案便转化为求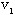 → → 的最短路。 的最短路。
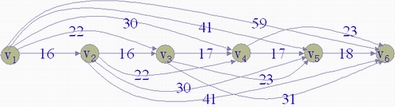
设d( )表示点 )表示点 到终点的最短距离,根据动态规划最优性原理,最短路径中任何子路径也必然是最短的。因此有 到终点的最短距离,根据动态规划最优性原理,最短路径中任何子路径也必然是最短的。因此有
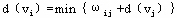
注意,上式要对以 为起点的所有弧( 为起点的所有弧( , ,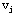 )进行计算。然后将计 )进行计算。然后将计
算结果直接标在图中点 的旁边,同时标出与点 的旁边,同时标出与点 最近的邻接点。先从点 最近的邻接点。先从点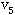 算起,逆向进行。 算起,逆向进行。
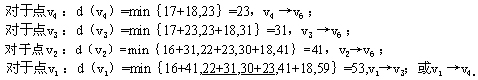
|

