第四节
网络最大流问题 (1)
(2)
4.2 计算最大流的标号法
这里介绍计算网络最大流的简便方法—标号法,此方法是Ford—Fulkerson
于1956年提出来的,它的原理是利用寻找增广链来不断改善可行流。
设μ是网络中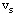 到 到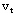 的一条链,规定 的一条链,规定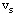 到 到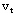 的方向为μ的方向。
μ上与μ的方向一致的弧称为前向弧,前向弧的集合记为μ+, μ上与μ的方向相反的弧称为后向弧,后向弧的集合记为μ-。 的方向为μ的方向。
μ上与μ的方向一致的弧称为前向弧,前向弧的集合记为μ+, μ上与μ的方向相反的弧称为后向弧,后向弧的集合记为μ-。
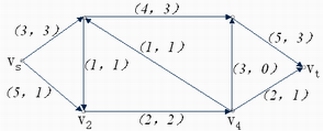
上图,链 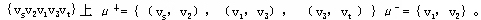
若给一个可行流{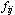 },称网络中 },称网络中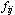 = =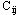 的弧为饱和弧,称 的弧为饱和弧,称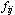 <
<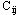 的弧为非饱和弧,称 的弧为非饱和弧,称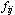 =0的弧为零流弧,称 =0的弧为零流弧,称
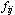 >0的弧为非零流弧。 >0的弧为非零流弧。
增广链:设{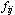 }是可行流,μ是 }是可行流,μ是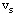 到 到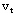 的一条链,若μ满足下列条件,则称μ为关于
f 的增广链。(注意: f ={ 的一条链,若μ满足下列条件,则称μ为关于
f 的增广链。(注意: f ={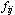 }) })
1°对于任何( ,
,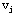 )∈μ+,0≤ )∈μ+,0≤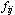 < <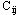 (前向弧为非饱和弧)
(前向弧为非饱和弧)
2°对于任何( ,
,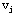 )∈μ-,0
< )∈μ-,0
<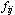 ≤ ≤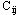 (后向弧为非零流弧)
(后向弧为非零流弧)
如图7-15中,μ={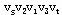 }就是一条增广链。 }就是一条增广链。
定理:可行流 f﹡是最大流,当且仅当不存在关于 f﹡的增广链。
证明:必要性:设 f﹡是最大流,若存在关于 f﹡的增广链μ,令
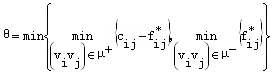
则θ >0,令
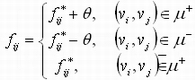
|

