第五节 单纯形法的进一步讨论   (1) (2)
    5.1 两阶段法
    对于前面介绍的大M法，如果用计算机求解时，只能用很大的正数代替M，这就可能造成计算上的错误。下面介绍不须要引进相当大正数M的两阶段法。
    第一阶段，求初始基可行解：在约束中添加人工变量，使约束矩阵出现单位子矩阵，然后以这些人工变量之和的相反数W求最大为目标函数，进行求解。若第一阶段最优解对应的最优值等于零，则所有人工变量一定都取零值，说明原问题存在基可行解，可以进行第二阶段计算，否则原问题无可行解，应停止计算。
    第二阶段，求原问题的最优解：将第一阶段计算得到的最终表，除去人工变量，恢复原来的目标函数，并以第一阶段的最优解为初始基可行解，重新计算检验数，然后用单纯形法继续求解。
    例9 用两阶段法求解下列线性规划
        
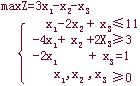
    解 加入松弛变量及人工变量，给出第一阶段数学模型：
        
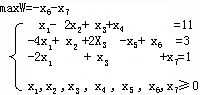
    取(P4,P6,P7)为初始基B，列出初始单纯形表，并计算如下：
        
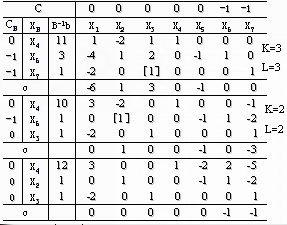
    因为最优解中人工变量均等于零，所以可以进行第二阶段计算。
        
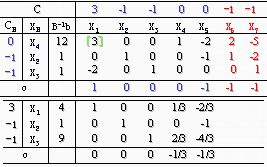
    由此得原问题最优解：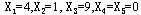
    最优值：Z=2