第一节 线性规划问题   (1) (2) (3)
    1.1 线性规划问题的数学模型
    线性规划是研究在一组线性不等式或等式约束下使得某一线性目标函数取最大（或最小）的极值问题。下面我们通过几个例子来介绍线性规划问题的数学模型。
    例1.某工厂生产Ⅰ，Ⅱ两种型号计算机，为了生产一台Ⅰ型和Ⅱ型计算机，所需要原料分别为2和3个单位，需要的工时分别为4和2个单位。在计划期内可以使用的原料为100个单位，工时为120个单位。已知生产每台Ⅰ，Ⅱ型计算机可获得利润分别为6和4个单位，试确定获利最大的生产方案。
    建立该问题的数学模型
    设X1,X2分别表示计划期内产品Ⅰ，Ⅱ的产量。因为计划期内生产用的原料和工时都是有限的，所以在确定产品Ⅰ，Ⅱ的产量时要满足下面约束条件:
            
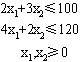
    一般满足上述约束方程组的解不是唯一的，根据题意我们需要的是既满足约束条件，又使得所获利润最大的方案。
    若以Z表示总利润，我们的目标是:
        
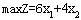
    综合上述，该问题可用数学模型表示为：
    目标函数：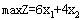
    约束条件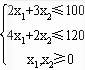：