第四节
单纯形法 (1) (2)
(3) (4) (5)
(6) (7) (8)
单纯形法的基本思想是:从可行域的一个基可行解(一个顶点)出发,判断该解是否为最优解,如果不是最优解就转移到另一个较好的基可行解,如果目标函数达到最优,则已得到最优解,否则继续转移到其他较好的基可行解。由于基可行解(顶点)数目有限,所以在一般情况下经过有限次迭代后就一定能求出最优解。
4.1 确定初始基可行解
对于线性规划问题 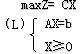
我们首先介绍求初始基可行解的方法。
1.直接观察法
若给定问题标准化后(且b≥0)系数矩阵A中存在m个线性无关的单位列向量,则以这m个单位列向量构成的单位子矩阵作为初始基B,则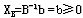 ,其余 ,其余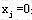 是基可行解。 是基可行解。
2.大M法(人工变量法)
若给定问题标准化后(b≥0)系数矩阵中不存在m个线性无关的单位列向量,则在某些约束的左端加一个非负变量(人工变量),使得变化后的系数矩阵中恰有m个线性无关的单位列向量,并且在目标函数中减去这些人工变量与M的乘积(M是相当大正数).对于变化后的问题,取这m个单位列向量构成的单位子矩阵为初始基,该基对应的解一定是基可行解.
显然,对任意形式的线性规划问题都可以用这种增加人工变量的方法“凑出”一个单位子矩阵作为初始可行基.
按这种方法变化得到的线性规划与原线性规划有如下关系:
⑴原问题的任一基可行解都是变化后的问题的基可行解.
⑵若变化后问题的最优解中不含有非零的人工变量,则该解就是原问题的最优解.
⑶若变化后问题的最优解中含有非零的人工变量,则原问题无可行解.
|

