第四节
单纯形法 (1) (2)
(3) (4) (5)
(6) (7) (8)
定理4.1(最优性判定定理) 对某基可行解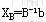 ,其余 ,其余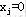 ,若所有检验数 ,若所有检验数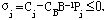
j=m+1,m+2,...,n 则该解为最优解。
证明 对一切可行解X,当所有检验数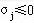 时 时
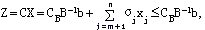
而基可行解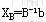 ,其余 ,其余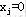 对应的目标函数值恰为 对应的目标函数值恰为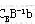 , ,
∴基可行解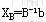 ,其余
,其余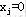 是最优解,B为最优基。 是最优解,B为最优基。
定理4.2(无界解判定定理) 若对某可行基B,存在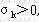 ,且 ,且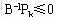 ,则该问题无有限最优解。 ,则该问题无有限最优解。
证明:设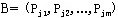 ,定义向量 ,定义向量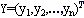 , ,
其中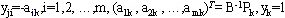 ,
其余 ,
其余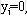
则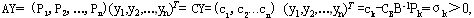 , ,
由Y的定义知Y≥0,所以,如果问题有可行解X,则对任何λ>0,
A(X+λY)=AX+λAY=b,即X+λY也是可行解。
故,当λ→+∞时,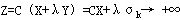 ,证毕。 ,证毕。
有了定理4.1,定理4.2后,对于线性规划的任何一个基可行解,只要通过计算检验数,就能够判断该解是否为最优解。
如 例1 标准化后变为 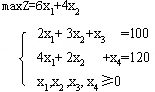
取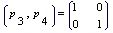 为初始基B, 为初始基B,
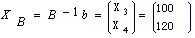 , ,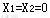 为初始基可行解。 为初始基可行解。
∵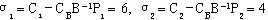
∴该解不是最优解。
|

