第三节
线性规划问题的几何意义 (1) (2)
(3)
定义(凸集) 设K是n维欧氏空间的一个点集,若任意两点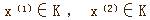 的连线上的一切点 的连线上的一切点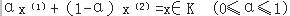
则称K为凸集。
凸集的特征是:连接集合中任意两点的线段整个地都在集合之中。实心的凸多边形、凸多面体都是凸集。
定义(凸组合) 设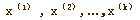 是n维欧氏空间的k个点,若存在满足 是n维欧氏空间的k个点,若存在满足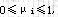 ,
i=1,2…k, 则称 ,
i=1,2…k, 则称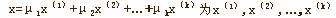 的凸组合. 的凸组合.
定义(顶点)设K是凸集,X∈K,若X不能表示成任何 两点连线的内点,则称X为K的一个顶点(或极点)。
两点连线的内点,则称X为K的一个顶点(或极点)。
关于线性规划问题解的性质,介绍以下几个定理:
定理3.1 线性规划的可行域 D={x︱Ax=b,x≥0}是一个凸集。
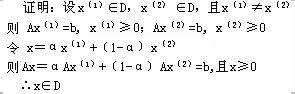
因此,根据凸集的定义,知D是凸集。 |

