第三节
线性规划问题的几何意义 (1) (2)
(3)
引理2 若K是有界凸集,则任何一点x∈K都可表示为K的顶点的凸组合。
定理3.3 若可行域非空有界,则线性规划问题一定可以在可行域的某个顶点上找到最优解。
证明:不妨设可行域的顶点为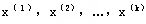
再设x(0)是可行域D的任意一点。由引理2,有
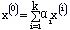 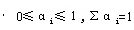
因此,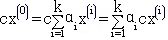
则有 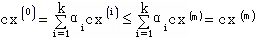
由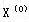 的任意性,知线性规划在顶点 的任意性,知线性规划在顶点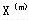 处达到最优。 处达到最优。
重要结论
根据以上讨论,可以得到以下结论:
线性规划问题的可行域是凸集(定理3.1);凸集的每个顶点对应一个基可行解(定理3.2),基可行解个数是有限的,当然凸集的顶点也是有限的;若线性规划有最优解,必在可行域某顶点上达到(定理3.3),亦即在有限个基可行解中间存在最优解。因此,我们可以在有限个基可行解中去找最优解。这就是下节将介绍的单纯形法的理论依据,该方法就是一种在基可行解中搜索最优解的算法。
|

