第三节
线性规划问题的几何意义 (1) (2)
(3)
引理1 线性规划的可行解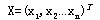 是基可行解的充要条件是:
X的正分量对应的系数列向量是线性无关的。 是基可行解的充要条件是:
X的正分量对应的系数列向量是线性无关的。
定理3.2 X是可行域D={x︱Ax=b,x≥0}的顶点的充要条件是:X是该线性规划问题的基可行解。
证明:
必要性→设X是D的顶点。若X不是基可行解,不妨设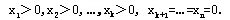 由引理1知 由引理1知
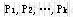 必线性相关,于是存在不全为0的一组数 必线性相关,于是存在不全为0的一组数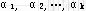 满足 满足
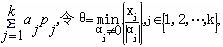
显然θ>0。
取
易于验证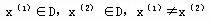 且 且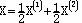 ,此与X是D的顶点矛盾,因而X是基可行解。
,此与X是D的顶点矛盾,因而X是基可行解。
充分性:←设X是问题的基可行解,不妨设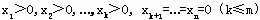 ,于是 ,于是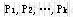 必线性无关。若X不是D的顶点,则存在有 必线性无关。若X不是D的顶点,则存在有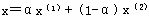 于是,对j=k+1,k+2,…,n,有
于是,对j=k+1,k+2,…,n,有 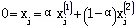
因此,对于j=k+1,k+2,…,n,应有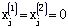
并且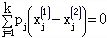 ,由于 ,由于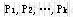 线性无关, 线性无关,
故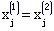 ,j=1,2,…,k.这就得到了 ,j=1,2,…,k.这就得到了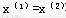 之矛盾。 之矛盾。
因此,X必为顶点。
|

