第四节
单纯形法 (1) (2)
(3) (4) (5)
(6) (7) (8)
4.4 基变换—(L,K)旋转变换(换基迭代)
在单纯形法中,如果得到的基可行解经检验不是最优解,又不能判定无有限最优解时,就应该去找一个新的基可行解。具体做法是从原可行基中撤换一个列向量(当然要保证撤换后的各列向量仍线性无关),得到一个新的可行基,这称为基变换。为换基,先要确定换入变量(进基变量)
,再确定换出变量(出基变量),让它们相应的系数列向量对换,进而便可求得一个新的基可行解。
⑴换入变量的确定:由目标函数的表达式,可以看出,当某个非基变量Xj的检验数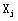 时, 时,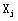 增加则目标函数值可以增大,这时应将 增加则目标函数值可以增大,这时应将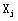 换为基变量。若有两个以上的,为了使目标函数值增加得快,从直观上一般选σj
>0中的最大者对应的非基变量作为换入变量。即 换为基变量。若有两个以上的,为了使目标函数值增加得快,从直观上一般选σj
>0中的最大者对应的非基变量作为换入变量。即
若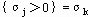 ,
,
则确定对应的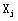 为换入变量。此法可称为最大σ(检验数)规则。 为换入变量。此法可称为最大σ(检验数)规则。
⑵换出变量的确定:将基B对应的单纯形表还原成约束方程组:
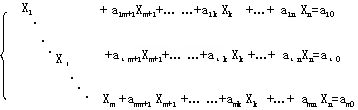
假设按最大σ规则已确定为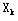 换入变量。现在要从基变量X1,X2,...,Xm
中确定一个换出变量,为了使新的解可行,对换后,必须仍保证 换入变量。现在要从基变量X1,X2,...,Xm
中确定一个换出变量,为了使新的解可行,对换后,必须仍保证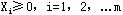 。在上述方程组中,除 。在上述方程组中,除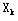 外,其余非基变量仍取0值,从而,应使 外,其余非基变量仍取0值,从而,应使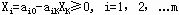 ,当
,当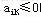 时,这是没有问题的,因此,只须考虑 时,这是没有问题的,因此,只须考虑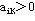 的情况,应使 的情况,应使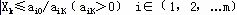 。故而,当取 。故而,当取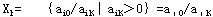
时,即可满足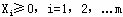 ,且有 ,且有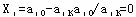 ,由此可见,可按 ,由此可见,可按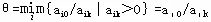 来确定对应的Xi(单纯形表第ι行的基变量)为换出变量。此法可称为最小θ(比值)规则。
来确定对应的Xi(单纯形表第ι行的基变量)为换出变量。此法可称为最小θ(比值)规则。
|

