第一节 线性规划问题   (1) (2) (3)
    例2 某昼夜服务的公交线路每天各时间区段内所需司机和乘务人员数如下：
        班次      时间         所需人数
        1     6：00—10：00     60
        2     10：00—14：00    70
        3     14：00—18：00    60
        4     18：00—22：00    20
        5     22：00— 2：00    20
        6     2：00— 6：00     30
    设司乘人员在各时间段一开始时上班，并连续工作8小时，问该公司线路至少应配备多少司乘人员。列出该问题数学模型。
    解: 设X1,X2 ,…,X6为各班新上班人数，考虑到在每个时间段工作的人数既包括该时间段新上班的人又包括上一个时间段上班的人员，按所需人员最少的要求可列出本例的数学模型：
    目标函数: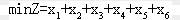
    约束条件: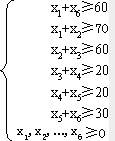
    上面两例优化模型，都具有下述特征：
    (1)每个问题都用一组未知变量X1,…,Xn表示所求方案，通常这些变量都是非负的，称为决策变量。
    (2)存在一组约束条件，这些约束条件都可以用一组线性等式或不等式表示。
    (3)都有一个要求的目标，并且这个目标可表示为一组决策变量的线性函数，称为目标函数。目标函数可以是求最大，也可以是求最小。 具有上述特征的数学模型就称为线性规划模型。
    线性规划数学模型的一般形式如下：
    目标函数：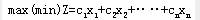
    约束条件: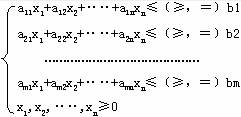