第一节 线性规划问题   (1) (2) (3)
    1.2 图解法
    如何求解线性规划模型是本章讨论的中心问题。 首先介绍只有两个决策变量的线性规划的图解法，该方法能够对线性规划的解法从几何直观上给我们以启迪。
    对于两个决策变量的每一组取值，都可以看作平面直角坐标系中一个点的坐标，因此，我们可以把满足约束条件的点在平面直角坐标系中表示出来。以例1的模型为例，约束条件2X1+3X2≤100，4X1+2X2≤120都代表由一条直线划定的半个平面，考虑到X1,X2≥0，所以，满足所有约束条件的点应为坐落在第一象限的区域OQ1Q2Q3（如图），该区域称为可行域。
                
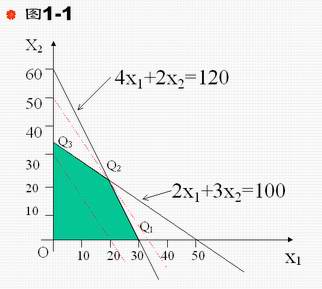
    决策变量的一组取值称为线性规划问题的一个解。满足约束条件的解称为可行解。所有可行解的集合即称为可行域。使目标函数达到最优的解称为最优解。
    例1的可行域包含无穷多个可行解，为了在无穷多个可行解中找到最优解，我们在坐标系中画出目标函数表示的一族平行线。观察这族平行线移动时对应的Z值变化,可以看出，这族平行线愈向右上方移动，对应Z值愈大。由于平行线族在Q2点脱离可行域，所以，例1在Q2点取得最优解。 Q2是直线2X1+3X2=100和4X1+2X2=120的交点，解此方程组可得 :X1=20,X2=20.因为例1的解是：生产Ⅰ型Ⅱ型计算机分别为20台，能得到最大利润为200单位。
    从图解法可以看出一般情况下
    （1）具有两个变量的线性规划问题的可行域是凸多边形。
    （2）若线性规划存在最优解，它一定在可行域的某个顶点得到。
    虽然图解法只能求解包含2个变量的问题，作为算法，没有太大价值，但是上述结论却非常有意义。它将搜索最优解的范围从可行域的无穷多个点缩小到有限几个顶点。这就开启了人们的思路。而后面我们要介绍的求解多维线性规划的单纯形法就是在此结论的基础上推广得到的。