第六节
线性规划应用举例 (1) (2)
(3)
例13 (投资问题) 某部门在今后五年内考虑给下列项目投资,已知:项目A,从第一年到第四年初需要投资,并于次年末回收本利115%;项目B,第三年初需要投资,到第五年末能回收本利125%,但规定最大投资额不超过4万元;项目C,第二年初需要投资,到第五年末能回收本利140%,但规定最大投资额不超过3万元;项目D,五年内每年初都可投资,于当年末归还,并加利息6%.
该部门现有资金10万元,问应如何确定这些项目的投资,使到第五年末拥有资金本利总额最大?
解: 这是个连续投资问题,按投资的时间要求,设各年初投资额如下表所示:
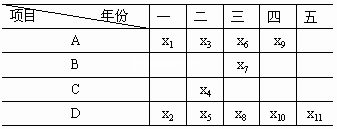
例14 某工厂有三个车间生产同一种产品。每件产品由4个零件1和3个零件2组成。这两种零件需耗用两种原材料。已知这两种原材料的供应量分别为300㎏和500㎏。由于三个车间拥有的设备及工艺条件不同,每个工班原材料耗用量和零件产量也不同,具体如下表所示。问三个车间应各开多少工班,才能使该产品的配套数达到最大?
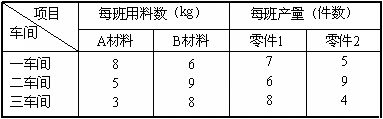
解:设X1,X2,X3分别为一、二、三叁个车间所开工班数,则
这三个车间所生产的零件1总数为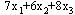 ,零件2总数为 ,零件2总数为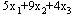 。要注意的是,本例的目的不是生产各种零件的总数最多,而是要求产品的配套数最大。因此,目标函数应为 。要注意的是,本例的目的不是生产各种零件的总数最多,而是要求产品的配套数最大。因此,目标函数应为
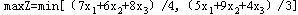
这个目标函数不是线性函数,可以通过恰当的变换将其变为线性函数:令,
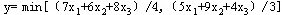
则此式与下面两个不等式等价:
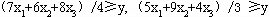
于是,本例的线性规划模型可以列出为:
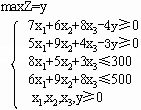
|

