第二节
对偶理论 (1)
(2)
性质3(弱对偶性) 设X,Y分别是原问题(L)和对偶问题(D)的任一可行解,则CX≤Yb
性质4 设 是原问题的可行解, 是对偶问题的可行解,且C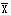 = =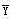 b
, 则 b
, 则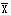 , ,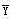 是各自问题的最优解。
是各自问题的最优解。
性质5 若原问题 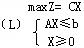
有最优解,则其对偶问题也有最优解,且它们的最优值相等。
证明:设B,X是原问题的最优基及最优解,记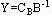 则有
则有
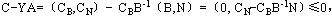 即YA≥C;再由AX≤b,可得
即YA≥C;再由AX≤b,可得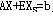 , ,
显然,松弛变量Xs的检验数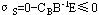 ,即 ,即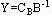 ≥0,所以,Y是对偶可行解。又
≥0,所以,Y是对偶可行解。又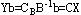
,知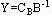 是对偶问题的最优解。 是对偶问题的最优解。
由证明过程可知:对偶最优解Y实际是原问题松 弛变量检验数的相反数。 |

