第五节
最小费用最大流问题 (1)
(2) (3) (4)
(5)
由于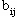 ≥0,所以
f ={0}必是流量为0的最小费用流。这样,总可以从 f ={0}开始算起。一般地,如果已知 f 是流量为v(f )的最小费用流,余下的问题就是如何去寻找关于
f 的最小费用增广链。 ≥0,所以
f ={0}必是流量为0的最小费用流。这样,总可以从 f ={0}开始算起。一般地,如果已知 f 是流量为v(f )的最小费用流,余下的问题就是如何去寻找关于
f 的最小费用增广链。
为此,构造一个有向费用网络W( f ),它的顶点与原网络完全相同,而把原网络中的每一条弧( ,
,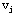 )分解成方向相反的两条弧,即( )分解成方向相反的两条弧,即( ,
,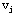 )和( )和(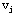 ,
, )。并按如下规则定义W( f )中弧的权数:
)。并按如下规则定义W( f )中弧的权数:
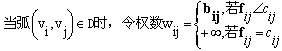

上述定义式的含义是:在增广链的前向弧上,当 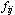 < <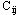 时,可以增加流量,其单位费用为
时,可以增加流量,其单位费用为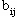 ,当
,当 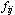 = =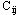 时不能再增加流量,否则要花费高昂的代价,因此单位费用为+∞。在增广链的后向弧上,当
时不能再增加流量,否则要花费高昂的代价,因此单位费用为+∞。在增广链的后向弧上,当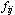 >0时,减少一个单位流量可节约的费用为 >0时,减少一个单位流量可节约的费用为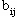 ,当
,当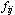 =0时,由于无法减少流量,因此单位费用亦为+∞。
=0时,由于无法减少流量,因此单位费用亦为+∞。
经上述处理后,在费用、容量网络中寻找关于 f 的最小费用增广链问题,就转化为在有向费用网络W(
f )中寻找从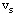 → →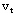 以费用表示的最短路。因是求最短路,故
= +∞的弧可以从网络中省略。 以费用表示的最短路。因是求最短路,故
= +∞的弧可以从网络中省略。
具体算法步骤如下:
⑴取0流为初始最小费用可行流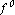 ,即v(
,即v(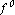 )=0;
)=0;
⑵若在k-1步(k=1,2, …)得最小费用流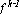 ,则构造关于 ,则构造关于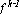 的有向费用网络W( 的有向费用网络W(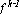 ); );
⑶在网络W(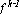 )中寻找从 )中寻找从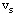 → →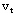 的最短路。若不存在最短路,则 的最短路。若不存在最短路,则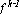 已是最小费用最大流,计算停止。否则转⑷; 已是最小费用最大流,计算停止。否则转⑷;
⑷在原网络图中与这条最短路相应的增广链上,对流量v(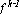 )进行调整,调整量为: )进行调整,调整量为: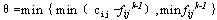
调整后得新的最小费用流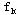 ,其流量为v( ,其流量为v(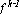 )+θ。用 )+θ。用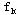 代替 代替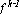 返回⑵
。 返回⑵
。 |

