第六节
M/G/1排队系统 (1)
(2) (3)
前两节讨论的模型是建立在生灭过程的基础上的,即假定到达和服务时间均为负指数分布的情况。但假定服务时间服从负指数分布往往与实际情况有较大出入。这里讨论M/G/1排队系统,即输入为普阿松流,服务时间为任意分布,具有单服务台的排队系统。
现在假定顾客平均到达率为λ,服务时间的期望值为1/μ,方差为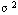 ,则可以证明:当ρ=λ/μ<1时,系统可以达到稳定状态,模型的几个主要参数的表达式如下: ,则可以证明:当ρ=λ/μ<1时,系统可以达到稳定状态,模型的几个主要参数的表达式如下:
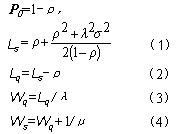
6.1 普阿松输入和定长服务时间的排队系统
当一个服务机构提供固定服务项目,服务时间偏差很小时,可以近似看作服务时间是定长分布。
定长分布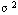 =0,代入前述公式得以下结果:
=0,代入前述公式得以下结果:
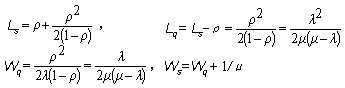
在服务时间为负指数分布的情况下,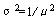 ,代入公式(1)有 ,代入公式(1)有
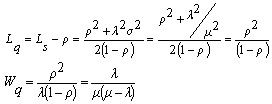
从公式可以看出,顾客等待的平均时间要比定长分布的大一倍,服务机构的效率差不多降低一倍。在平均服务时间1/μ一定的情况下,从公式(1)还可以看出,Ls,Lq,Wq,Ws均随的增加而增加,即服务时间分布的偏差越大,工作指标就越差,而对每个顾客的服务时间越接近,系统的工作指标就越好。定长分布的
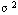 =0,所以它的Lq和Wq最小。 =0,所以它的Lq和Wq最小。
|

