第四节 单服务台排队系统模型(M/M/1)     (1) (2) (3) (4) (5) (6)
    本节将讨论输入为普阿松流，服务时间为负指数分布的单服务台排队系统模型。因为这类模型都符合生灭过程，所以可以将生灭过程的结论搬过来应用。
    下面分几种类型来讨论。
    4.1 M/M/1/∞/∞模型
    该模型是指顾客按普阿松流到达，到达速率为λ ，服务时间服从负指数分布，服务速率为μ ，单个服务台，系统对顾客无限制，顾客源也无限制，先到先服务的服务系统。其系统状态是无限的，即n=0，1，2，…。下图表示系统的状态转移图。
        
    因为对所有状态n ，λn=λ，μn=μ，所以
        
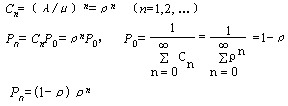
    这里ρ=λ/μ＜1是单位时间顾客平均到达率与平均服务率的比值,反映了服务机构的忙碌或利用程度,称ρ为服务强度或服务的忙期。因为ρ≥1时，系统内顾客数会越来越多，系统无法进入稳定状态，所以设ρ＜1。
    下面推导服务系统的其它指标：
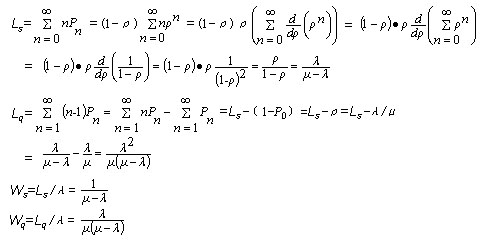