第四节
单服务台排队系统模型(M/M/1) (1)
(2) (3) (4)
(5) (6)
例2 某个单人理发店,备有六张椅子供顾客等待理发。当椅子坐满时,后来的顾客不再进入而自动离去。已知平均每小时到达3名顾客,每名顾客理发时间平均是15分钟。试求
⑴顾客无需等待就可理发的概率;
⑵店内顾客平均数;
⑶有效到达率;
⑷需要等待的顾客平均数;
⑸顾客在店内平均逗留时间;
⑹顾客等待理发的平均时间;
⑺有百分之几的顾客因客满而自动离去。
解:这个问题可以归结为M/M/1/7/∞模型, λ=3(人/小时),μ=4(人/小时),据此可以求出:
⑴顾客无需等待就可理发的概率:P0=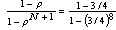 ≈0.2778 ≈0.2778
⑵店内顾客平均数: Ls 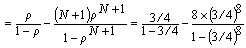 ≈2.11(人) ≈2.11(人)
⑶有效到达率: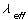 =μ(1-P0)=4×(1-0.2778)≈2.89(人/小时) =μ(1-P0)=4×(1-0.2778)≈2.89(人/小时)
⑷需要等待的顾客平均数: Lq=Ls-(1-P0)≈2.11-1+0.28=1.39(人)
⑸顾客在店内平均逗留时间: Ws=Ls / 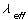 =2.11÷2.89≈0.73(小时)=43.8(分) =2.11÷2.89≈0.73(小时)=43.8(分)
⑹顾客等待理发的平均时间: Wq=Ws-1/μ =43.8-15=28.8(分)
⑺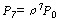 =(3/4)7×0.2778≈0.037=3.7% =(3/4)7×0.2778≈0.037=3.7%
|

