第二节
到达间隔与服务时间的分布 (1)
(2) (3)
解决排队问题首先要判断顾客到达间隔和服务时间的分布,现在介绍排队模型中常见的几种理论分布。
2.1 普阿松流
令Pn(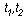 )表示在时间区间[ )表示在时间区间[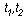 )( )(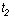 > >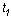 )内有n
个顾客到达的概率,当Pn( )内有n
个顾客到达的概率,当Pn(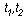 )和乎下列三个条件时,我们说顾客的到达形成普阿松流。 )和乎下列三个条件时,我们说顾客的到达形成普阿松流。
⑴无后效性。在不相重叠的时间区间内顾客到达数是相互独立的。
⑵平稳性。对充分小的△t,在时间区间[t,t+△t)内有1个顾客到达的概率与t无关,而与△t
成正比,即 P1(t,t+△t)=λ△t+ο(△t) 。其中 λ>0是常数,它表示单位时间有一个顾客到达的概率; ο(△t)是当△t→0时
,关于△t的高阶无穷小量。
⑶普通性。对于充分小的△t,在时间区间[t,t+△t)内有2个或2个以上顾客到达的概率极小,即
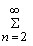 Pn(t,t+△t)=ο(△t) Pn(t,t+△t)=ο(△t)
根据普阿松流的三个条件,我们来讨论在[0,t)内顾客到达数N(t)的概率分布。
将长度为t 的时间区段分成n等份,△t =t/n,当n→∞时,△t为充分小,在△t内可能会有1个顾客到达,其概率为λ△t=λt/n,在△t内也可能没有顾客到达,其概率为
1-λ△t=1-λt/n 。
记[0,t)内有k个顾客到达的概率为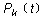 , ,
则 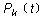 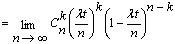
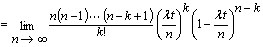
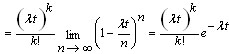
k =0,1,2, … |

