第二节
到达间隔与服务时间的分布 (1)
(2) (3)
由于普阿松流与实际流的近似性,更由于普阿松流容易处理,因此排队论中大量研究的是普阿松流情况。事实上,应用排队论来研究实际问题到目前为止也主要限于普阿松流,对非普阿松流的情况,大多还没有得到满意的分析解。
2.2 负指数分布
在实际排队系统中服务时间的概率分布可以是各种形式,但在排队论中,最容易进行数学处理、最常用的一种重要分布是负指数分布。设T是一个以μ为参数的负指数分布,它的概率密度函数为:
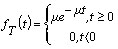
它的分布函数是 P{T≤t}= 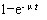 (t>0) (t>0)
数学期望E(T)=1/μ,方差D(T)=1/ 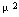
负指数分布具有下列性质:
⑴由条件概率公式容易证明 P{T > t+s|T>s}=P{T>t}
这个性质称为无记忆性或马尔可夫性。若T表示排队系统中顾客到达的间隔时间,那么这个性质说明一个顾客到达所需的时间与过去一个顾客到达所需的时间s无关,所以这种情况下的顾客到达是纯随机的。
⑵当输入过程是普阿松流时,相继到达的顾客的间隔时间T服从负指数分布。
事实上,对于普阿松流,若顾客到达的间隔时间T≤t,则在[0,t)内至少有1个顾客到达,从而
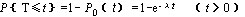
即T服从参数为λ的负指数分布。
因此,相继到达的间隔时间是独立且为相同参数的负指数分布,与输入过程为普阿松流(参数为λ)是等价的。
根据负指数分布与普阿松流的关系可以推出,当服务机构对顾客的服务时间服从参数为μ的负指数分布,如果服务机构处于忙期,则该服务机构的输出,即服务完毕离开服务机构的顾客数将是服从普阿松分布的普阿松流。其中μ为每个顾客的平均服务时间,也是顾客相继离开的间隔。
|

