第四节 单服务台排队系统模型(M/M/1)     (1) (2) (3) (4) (5) (6)
    4.3 M/M/1/∞/m 模型（顾客源有限）
    现在来分析顾客源有限的排队问题。这类排队问题的主要特征是顾客总数是有限的，如只有m个顾客。每个顾客来到系统中接受服务后仍回到原来的总体，还有可能再来。这类问题在工业生产中遇到的较多，最典型的例子是机器看管问题。如一个工人同时看管m台机器，当机器发生故障时即停下来等待修理，修好后再投入使用，且仍然可能再发生故障。类似的例子还有m个打字员共用一台打字机，m个终端共用一台打印机等等。
    关于顾客的平均到达率，在无限源的情形中是按全体顾客来考虑的，而在有限源的情形下，必须按每一顾客来考虑。假定每个顾客来到服务系统的时间间隔均服从参数为λ的负指数分布，则λ表示单个顾客的平均到达率（其含义是指单位时间内该顾客来到系统请求服务的次数）。当顾客总数为m ，而系统内有n个顾客时，顾客总的平均到达率为(m-n)λ,因此顾客源有限的排队模型也可以用生灭过程的状态转移图来表示如下：
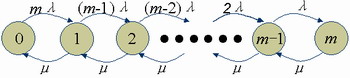
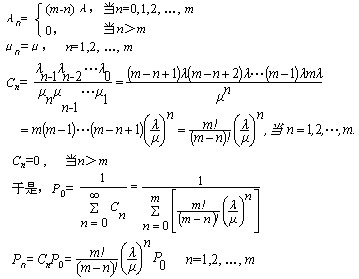