第四节
单服务台排队系统模型(M/M/1) (1)
(2) (3) (4)
(5) (6)
下面再计算:顾客在系统中停留时间超过t的概率是多少?假定一个顾客来到系统时,系统中已有n个人,则该顾客在系统中的停留时间应该是系统对前n个顾客的服务时间加上对他的服务时间。若分别用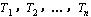 表示前n个顾客的服务时间, 表示前n个顾客的服务时间,
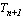 表示对该顾客的服务时间,令 表示对该顾客的服务时间,令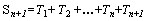 ,则
,则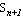 满足n+1阶爱尔朗分布,参数为μ。 满足n+1阶爱尔朗分布,参数为μ。
可以证得其密度函数为
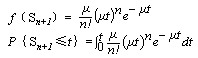
顾客在系统中停留时间小于t的概率
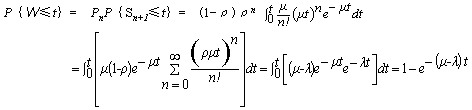
即W服从参数为μ-λ的负指数分布。
所以顾客在系统中停留时间大于t的概率
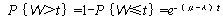
例1 某超级市场,顾客按普阿松流来到唯一的收款台。已知平均每小时来到20人,记价收款时间服从负指数分布,平均每个顾客需2.5分钟,试求该超级市场收款台的有关运行指标。
解:根据题意,这是M/M/1/∞/∞模型,
λ=20/60=1/3,μ=1/2.5,ρ=λ/μ=5/6
系统有关指标计算如下:
⑴ 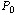 =1-ρ=1-5/6=1/6,忙期概率为
1- =1-ρ=1-5/6=1/6,忙期概率为
1-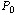 =ρ=5/6 =ρ=5/6
⑵系统内顾客平均值 Ls=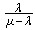 =1/3÷(1/2.5-1/3)=5(人)
=1/3÷(1/2.5-1/3)=5(人)
⑶排队等待顾客平均值Lq=Ls-λ/μ=5-5/6=4.167 (人)
⑷每个顾客在系统内平均逗留时间 Ws=Ls /λ=5÷(1/3)=15(分钟)
⑸每个顾客在队列中平均逗留时间Wq= Ws-1/μ=12.5(分钟) |

