第四节 单服务台排队系统模型(M/M/1)     (1) (2) (3) (4) (5) (6)
    4.2 M/M/1/N/∞模型
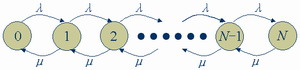
    在实际生活中经常会碰到队长有限制的服务系统，如医院规定每天挂100个号，那么第100个以后到达者会自动离开服务系统；理发店内等待的座位都满员时，后来的顾客就会离开，等等。因为队长有限制，所以系统的状态只能取0，1，2，…，N这些值。系统状态转移图如下图所示。
    
    
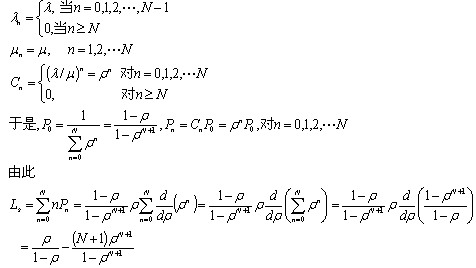
    与M/M/1/∞/∞模型中的Ls比较，两个表达式第一项相同，差别是多了一项：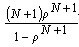
    由于ρ＜1 ，容易看出：在队长受限制情况下，系统中顾客数一定小于队长不受限制时系统中的顾客数；另外当N→∞时，Ls→ ，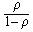
    与队长不受限制时系统中的顾客平均数完全一致。因此，队长不受限制系统可看作队长受限制系统的一种特例。
    为了计算系统其它各项指标，先要引进有效输入率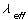 的概念。
    因为在队长受限制的情况下，当到达的顾客数n≥N时，新来的顾客会自动离去。因此虽然顾客以平均为λ的速率来到服务系统，但由于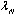=0，真正进入服务系统的顾客平均输入率却是小于λ的 。
    
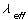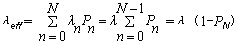
    可以验证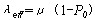
    由此可以算得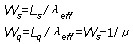：