第五节 均数的抽样误差和总体均数的估计
(1) (2)
(3) (4) (5)
(6) (7)
一、均数的抽样误差与标准误
㈠ 均数的抽样误差
由于总体常常不能直接研究,因此从总体中随机抽取一定数量的观测值作为样本进行抽样研究(sampling
study)成为统计研究的最基本的方法。变异的存在使得样本指标与总体指标不一定恰恰相等。这种由抽样造成的统计量与总体参数的差异叫抽样误差。抽样误差是不可避免的。
㈡ 标准误
研究抽样误差的大小的变化规律对于由样本指标推断总体指标非常有意义。
统计学基础理论的中心极限定理指出:
① 从正态分布总体 中随机抽取容量为n的样本,其样本均数 中随机抽取容量为n的样本,其样本均数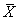 服从正态分布
。其中 服从正态分布
。其中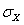 可按下式计算: 可按下式计算:
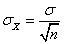 公式(10.19)
公式(10.19)
② 如果一个变量的总体分布具有均数μ和标准差σ,则从该总体抽得的容量为n的样本,在n趋于无穷大时,样本均数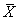 的分布趋向正态分布 的分布趋向正态分布 。 。
定理的直观表述见下图。 |
|


