第一节 直线回归
(1)
(2) (3) (4)
(5) (6) (7)
(8) (9)
附 五、直线回归方程的应用
㈠ 描述两变量依存关系
通过回归系数的假设检验，若认为两变量间存在直线回归关系，则可用直线回归方程来描述两变量间依存的直线定量关系。如例13.1求得的直线回归方程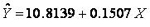 就是该地女性年龄对收缩压的直线定量表达式。
㈡ 利用回归方程进行统计预测
这是回归方程的重要应用方面。所谓统计预测(statistical forecast)就是把预报因子(自变量X)代入回归方程对预报量(应变量Y)进行估计，其波动范围可按求个体Y
值的容许区间方法计算。
㈢ 利用回归方程进行统计控制
统计控制(statistical control)就是利用回归方 程进行逆估计，如要求应变量Y在一定范围内波动，可以通过自变量X的取值来实现。
附 五、应用直线回归的注意事项
1. 作回归分析要有实际意义 不能把毫无关联的两个事物或现象拿来作回归分析，如身高与血压之间作回归分析，即便二者有回归关系，也不一定是因果关系，或者这种回归关系没有实际意义。
2. 作直线回归分析前，应绘制散点图 只有当点的分布具有直线趋势时，才适合作直线回归分析。散点图还可提示数据中有无异常点(outlier),即对应于残差绝对值特别大的观测点数据。异常点的存在往往对回归方程中的系数a、b的估计影响较大。
3. 直线回归方程的适用范围一般以自变量的取值范围为限，应避免外延 因为在自变量取值范围以外，两变量之间不一定存在同样的直线关系。
|
|
