第二节 线性规划问题的标准型与解的概念   (1) (2) (3) (4)
    2.2 线性规划解的概念
    我们把决策变量的一组取值称为线性规划问题的一个解。满足约束条件的解称为可行解。所有可行解的集合称为可行域。使目标函数达到最优的可行解称为最优解。
    在上一节图解法中，我们求得例1问题的最优解是唯一的，但是线性规划问题的解还可能出现以下几种情况：
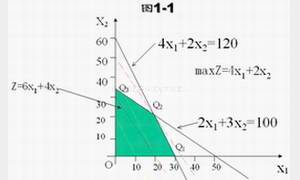
    （1）无穷多个最优解。若例1的目标函数变为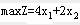 ，就会出现这种情况。见图1-1。
                
    （2）无可行解。如果约束中存在相互矛盾的约束条件，则导致可行域是空集，此时问题无可行解。
    （3）无有限最优解。对下述线性规划问题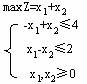
    用图解法求解结果见图1-2。
                
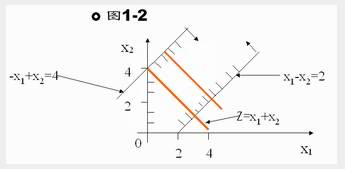
    从图中可以看出可行域无界，在可行域中找不到最大值点，目标函数值可以增大到无穷大，称这种情况为无有限最优解或无界解。