第二节
线性规划问题的标准型与解的概念 (1)
(2) (3) (4)
线性规划基解的概念
记线性规划问题为 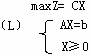
基:设A是m×n阶约束系数矩阵(m≤n),秩A=m. 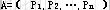 ,则A中一定存在m个线性无关的列向量,设为 ,则A中一定存在m个线性无关的列向量,设为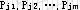 ,称可逆矩阵B=( ,称可逆矩阵B=(
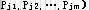 为线性规划(L)的一个基,称B中的列向量对应的变量 为线性规划(L)的一个基,称B中的列向量对应的变量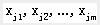 为基变量,其余变量称为非基变量。
为基变量,其余变量称为非基变量。
基本解:记基变量为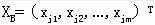 ,非基变量构成的列向量记为 ,非基变量构成的列向量记为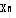 ,并令 ,并令
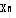 =0,则有 =0,则有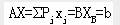 ,于是有 ,于是有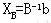 。称
。称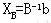 , ,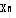 =0为线性规划(L)的一个基本解。 =0为线性规划(L)的一个基本解。
基可行解:若基本解中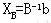 ≥0,则称该解为基可行解,这时基B也称为可行基。 ≥0,则称该解为基可行解,这时基B也称为可行基。
显然,基可行解的数目≤基解的数目≤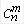
例4 求出下面线性规划的所有基本解,并指出哪些是基可行解。
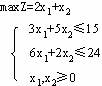
解 :标准化得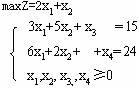
系数矩阵 

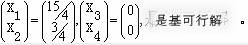
同理,取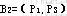 ,可得 ,可得
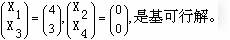
取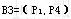 ,可得 ,可得

取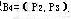 ,可得 ,可得
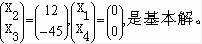
同理,取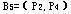 ,可得 ,可得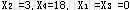 是基可行解。 是基可行解。
同理,取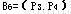 ,可得 ,可得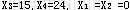 是基可行解。 是基可行解。
|

