第一节
资源分配问题 (1)
(2) (3)
给定一定数量的某种资源,例如人力、资金、设备、材料等,将其投入多种活动,就会产生如何分配资源给各项活动,使投放资源的总效果最优的问题,这就是资源分配问题。资源分配是相当广泛的经济问题,我们前面介绍的线性规划、整数规划、指派问题等都可以看作是求解资源分配的方法。这节介绍的资源分配问题是用前述方法难以解决,但由于其自身特点决定,可以用动态规划求解的实际问题。
现在设有某种资源(例如电、煤等)可用于n项活动,假设资源的数量为a,已知用于第i项活动的资源数为xi时,可以得到的收益为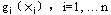 。试确定资源的分配方案使总收益最大。 。试确定资源的分配方案使总收益最大。
该问题的数学模型可以表示为:
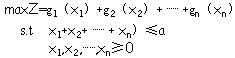
当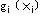 是线性函数时,该问题是线性规划问题;当 是线性函数时,该问题是线性规划问题;当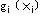 是非线性函数时,是非线性规划问题
,如果采用非线性规划方法去求解是比较麻烦的。然而由于这类问题的特点,可以将它看成一个多阶段决策问题,并利用动态规划方法求解。 是非线性函数时,是非线性规划问题
,如果采用非线性规划方法去求解是比较麻烦的。然而由于这类问题的特点,可以将它看成一个多阶段决策问题,并利用动态规划方法求解。
在应用动态规划方法去处理这一类资源分配问题时,通常将资源分给每项活动的过程看作一个阶段,每个阶段都要确定对一种活动的资源投放量。
这时,状态变量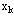 可选择k阶段初所拥有的资源量,即 可选择k阶段初所拥有的资源量,即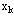 是要在第k项到第n项活动间分配的资源量。
决策变量 是要在第k项到第n项活动间分配的资源量。
决策变量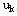 常常选对活动k的资源投放量,决策变量的允许集合是:
0≤ 常常选对活动k的资源投放量,决策变量的允许集合是:
0≤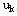 ≤ ≤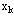
在选取上述状态变量和决策变量的情况下,状态转移方程是: 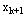 = =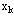 -
-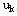 取投放资源时的效益为指标函数,则
取投放资源时的效益为指标函数,则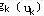 为阶段效益指标。 为阶段效益指标。
设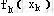 为k阶段到n阶段按最优分配方案获得的最大收益,
则动态规划基本方程是: 为k阶段到n阶段按最优分配方案获得的最大收益,
则动态规划基本方程是:
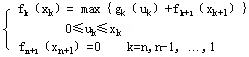
按基本方程,逆序计算,就可求得这类资源分配问题的最优解。 |

