第八节
其它应用问题
有些求最优解的问题,初看起来似乎不是多阶段决策问题,但经过适当变换后仍能变为多阶段决策问题,从而可用动态规划方法求解。
例10 求解下面的规划问题:

这是一个单约束条件的非线性规划问题,可以用非线性规划方法求解。现在把它转换成动态规划模型。就问题的模型来看,类似资源分配问题,约束条件右端常数相当于资源总量,三个变量可以看成是分三个阶段分配已有资源,Z是分配后的总效果。
令 k代表阶段, k=1,2,3;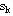 为状态变量,代表k阶段初尚未分配的资源总数; 为状态变量,代表k阶段初尚未分配的资源总数;
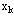 为决策变量,代表分配给第k阶段的资源量; 为决策变量,代表分配给第k阶段的资源量;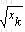 代表第k阶段决策确定后的直接效果。
代表第k阶段决策确定后的直接效果。
于是,状态转移方程为: 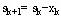
记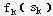 为k阶段到第3阶段按最优分配方案获得的最大效果,
则动态规划基本方程是: 为k阶段到第3阶段按最优分配方案获得的最大效果,
则动态规划基本方程是:
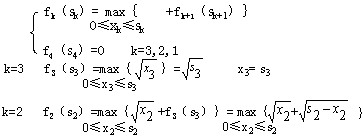
用微分法可求得上式当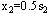 时,有最大值: 时,有最大值:
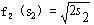
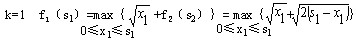
用微分法可求得上式当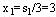 时,有最大值: 时,有最大值:
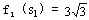
因此,原问题的最优解为: 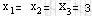 ,最优值为: ,最优值为:
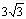
|

