第六节
排序问题 (1) (2)
(3)
设有n个不同零件 需要在m台不同机床 需要在m台不同机床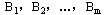 上加工,每个零件都必须依次经过 上加工,每个零件都必须依次经过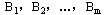 各道加工工序。 各道加工工序。
已知零件Ai在机床Bj上的加工时间(i=1,2…n;j=1,2…m),问应如何确定各零件的加工顺序,使在第一台机床B1上加工第一个零件开始到在第m台机床Bm上将最后一个零件加工完为止,所用的总时间最少?这就是所谓的m×n同序加工的排序问题。对于m≥3的排序问题,目前尚无有效解法,而对于只有两个工序,即m=2的排序问题,可以用动态规划方法加以解决。本节我们就讨论它的解法。
设n个不同零件依次在机床A、B上加工,用ai、bj分别表示零件i在A、B上的加工时间。
n个零件在机床A上有个加工顺序,在机床B上也有个加工顺序,不难证明,使得总工期最少的加工顺序,一定在A、B机床上具有相同的加工顺序。
事实上,若顺序不一样,在A上加工完的某零件不能马上在B上加工,而要等到另一个或一些零件在B上加工完后,才能加工,这势必使B的等待加工时间加长,从而使总的加工时间延长。
当加工顺序取定后,在机床A上没有等待时间,而在机床B上则常常等待。因此,寻找最优排序方案只有尽量减少在机床B上等待加工的时间。
现在我们以在机床A上更换零件的时刻为阶段 k=1,2,…n.
以X表示在机床A上等待加工的零件集合;以x表示不属于X 的在A上加工的零件;以t表示在A上加工完x时刻算起到B上加工完x所需时间。这样在A上加工完一个零件后,就有(X,t)与之对应,选取(X,t)作为描述加工过程的状态变量。
令f(X,t)表示由状态(X,t)出发,对未加工的零件采取最优加工顺序后,将X中所有零件加工完所需的时间。
令f(X,t,i)表示由状态(X,t)出发,在A上先加工零件i ,然后再对以后的零件采取最优加工顺序后,将X中所有零件加工完所需的时间。注意,这时t表示从零件i-1在A上加工完的时刻算起直到在B上把它加工完所需的时间。
令f(X,t,i,j)表示由状态(X,t)出发,在A上相继加工零件i,j,然后再对以后的零件采取最优加工顺序后,将X中所有零件加工完所需的时间。
于是,不难得到

其中X/i表示集合X去掉i后剩下的零件集合。
|

