第七节
货郎担问题 (1) (2)
货郎担问题也称旅行员问题,是运筹学里一个著名问题。设有n个城市,以1,2,…,n表示,表示从i城到j城的距离。一个推销员从城市1出发到其它每个城市去一次且仅仅一次,然后回到城市1,问他应如何选择行走路线,使总的路程最短。这个问题属于组合最优化问题,目前尚无有效解法。如果用穷举法,计算次数为n!,当n很大时,例如n=20,计算次数 实际上这是无法计算的。但当n不太大时,利用动态规划方法求解却是很方便的。 实际上这是无法计算的。但当n不太大时,利用动态规划方法求解却是很方便的。
规定推销员是从城市1出发,设推销员走到i城,s表示到达i城之前中途所经过的城市集合。选取(i,s)作为描述过程的状态变量,定义 为从1城出发经由k个中间城市的s集到i城的最短路线的距离,则 为从1城出发经由k个中间城市的s集到i城的最短路线的距离,则
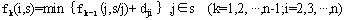
边界条件为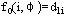 记最优决策函数为 记最优决策函数为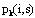 ,它表示从1城出发经k个中间城市的s集到i城的最短路线上紧挨着i城前面的城市。这样,我们可以从k=0出发,依次求出 ,它表示从1城出发经k个中间城市的s集到i城的最短路线上紧挨着i城前面的城市。这样,我们可以从k=0出发,依次求出 直至求出 直至求出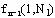 其中N1表示从1城出发回到1城的所有中间城市集合。
其中N1表示从1城出发回到1城的所有中间城市集合。
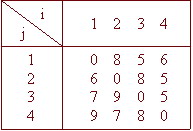
例9 求解四个城市的推销员问题,其距离矩阵如下表所示:
|

