第二节
树与最小部分树 (1)
(2) (3) (4)
从树的定义可以推出以下几点性质:
性质1 设T=(V,E)是一个树,p(T)≥2,则T中至少有两个悬挂点。
证明:令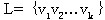 是T中含边数最多的一条链,因p(T)≥2,故链L中至少含两个点,从而 是T中含边数最多的一条链,因p(T)≥2,故链L中至少含两个点,从而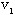 ≠ ≠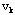 。现在证明v1是悬挂点,即d( 。现在证明v1是悬挂点,即d(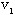 )=1。若d( )=1。若d(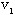 )
≥2,则至少存在边[ )
≥2,则至少存在边[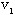 , ,
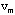 ],使m
≠ 2.若 ],使m
≠ 2.若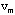 不在L上,则{ 不在L上,则{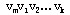 }是比L多一条边的链,与L是含边数最多的链矛盾。若 }是比L多一条边的链,与L是含边数最多的链矛盾。若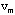 在L上,则{ 在L上,则{ }是T中的一个圈,这与T是树矛盾,于是必有d( }是T中的一个圈,这与T是树矛盾,于是必有d(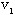 )=1,即 )=1,即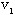 是悬挂点。同理可证 是悬挂点。同理可证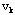 也是悬挂点。 也是悬挂点。
性质2 含有p个顶点的树中恰有p-1条边。
证明:当p=1,2时,结论显然成立。
假设p=k时结论成立,即有k-1条边。当p=k+1时,去掉一个悬挂边及与它关联的悬挂点,显然所得图仍是树,而且含有k个顶点k-1条边,所以,p=k+1的树应有k条边。综上,由数学归纳法,结论得证。
性质3 图G是树的充要条件是任意两点之间有且仅有一条链。
2.2 图的部分树
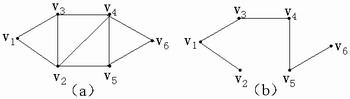
定义:设图T=(V,E′)是图G=(V,E)的部分图,如果是T=(V,E′)是树,则称T为G的部分树。
例如下图中,(b)是(a)的一个部分树。
|

