第二节
树与最小部分树 (1)
(2) (3) (4)
定理3 图G有部分树的充分必要条件是图G是连通图。
证明:必要性是显然的。
充分性:设图G是连通图,如果G不含圈,那么G本身是树,从而G是它自身的部分树。若G含圈,任取一个圈,去掉圈上的任一条边,则余下的图仍是连通图,如果这时图中无圈,则已得G的一个部分树,否则重复以上作法,最终可得到G的一个部分树。
定理3的证明提供了一个寻找部分树的方法,即
破圈法:在连通图G中任取一个圈,去掉圈上的任一条边,对余下的图重复这个步骤,直至无圈为止。
还可以采取另外的方法寻找部分树。
避圈法:每次增加一条边e ∈E,且与已有边不构成圈,直至恰有p-1条边为止。
2.3 最小部分树
定义:给图G=(V,E),对G的每条边[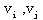 ],相应有一个数 ],相应有一个数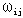 ,则称这样的图G为赋权图,称
,则称这样的图G为赋权图,称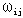 为边[ 为边[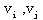 ]上的权。 ]上的权。
这里所说的“权”,根据实际问题需要,可以赋予它不同的含义,例如表示距离、时间、费用等等。赋权图不仅指出各个点之间的邻接关系,而且也表示出各点之间的数量关系。所以赋权图在工程技术及科学管理中有广泛的应用。
最小部分树就是赋权图上最优化问题之一。 |

