第二节
树与最小部分树 (1)
(2) (3) (4)
定义:给连通图G=(V,E),对每一边e∈E,有一权ω≥0,最小部分树问题就是求一个部分树T﹡,使
ω(T﹡)= 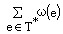 达到最小。 达到最小。
和求部分树一样,求最小部分树也有破圈法和避圈法。
破圈法:每次去掉圈上权数最大的边,直至无圈为止。
避圈法:每次取权数最小且与已取的边不构成圈的边,直至恰有p-1条边为止。
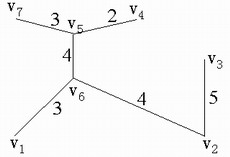
例1 今要在七个城市之间修筑一个公路网,每两个城市之间的公路修筑费用就是各条边上的权,见下图。试求总修筑费用最小的公路网。
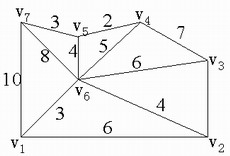
解:⑴破圈法:从圈{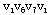 }中去掉边[ }中去掉边[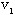 ,];从圈{
,];从圈{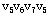 }中去掉边[ }中去掉边[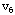 ,];从圈{
,];从圈{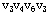 }中去掉边[ }中去掉边[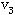 ,
,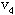 ];从圈{ ];从圈{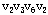 }中去掉边[ }中去掉边[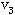 ,
,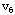 ];从圈{ ];从圈{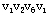 }中去掉边[ }中去掉边[
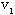 , ,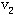 ];从圈{ ];从圈{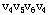 }中去掉边[ }中去掉边[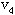 ,
,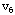 ],得最小树T﹡如下图,其总权数为ω(T﹡)=2+3+4+3+4+5=21。 ],得最小树T﹡如下图,其总权数为ω(T﹡)=2+3+4+3+4+5=21。
⑵避圈法:依次选取边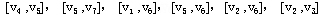 ,画出这棵最小树仍同下图。 ,画出这棵最小树仍同下图。
|

