第四章 数据分布特征的测度

 设众数组的频数为 f ，众数前一组的频数为 f-1 ，众数后一组的频数为 f+1 ，总众数组直方图的两个顶角向相邻两组直方图的两个顶角引直线，再由交叉点向横轴引垂线，与横轴相交的点即为众数。由图 4 － 1 可以看出，当众数相邻两组的频数相等时，即 f-1=f+1 ，众数组的组中值即为众数的值，如图4－1(a)所示；

当众数组前一组的频数多于众数组后一组的频数时，即 f-1>f+1 ，则众数会向前一组靠，众数小于其组中值，如图4－1(b)所示;

当众数组后一组的频数多于众数组前一组的频数时，即 f-1<f+1 , 则众数会向其后一组靠，众数大于其组中值，如图4－1(c)所示。

根据这种关系，可以利用相似三角形推导出分组数据众数的计算公式如下：

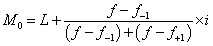式4－1

L 为众数组的下限值； I 为众数组的组距。

从分布的角度看，众数时具有明显集中趋势点的数值，一组数据分布的最高峰点所对应的数值即为众数。当然，如果数据的分布没有明显的集中趋势或最高峰点，众数也可能不存在；如果有两个最高峰点，也可以有两个众数。众数的示意图见图 4 － 2 。

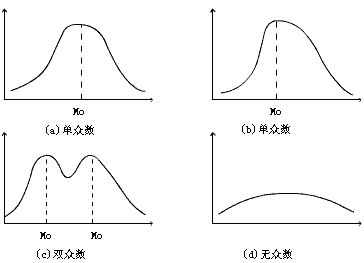
图4－2

众数的性质：

不受极端值影响的优点和没有利用所有观测值、缺乏敏感性和不适合代数运算的缺点。当资料是按品质标志分组时，用众数十分恰当。如果资料中有两个或多个众数，说明总体不是同质总体，将男、女混合计算身高，就会出现双众数的情形。