第四章 数据分布特征的测度

第一节 集中趋势的测度

<二>均值的另一种表现形式：调和平均数

调和平均数（ Harmonic mean ）也称调和均值，是均值的另一种表现形式。在实际工作中，由于所获得的数据不同，有时不能直接采用均值的计算公式来计算平均数，这就需要使用调和平均数的形式进行计算。式4－7就式调和平均公式：

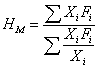，式4－8

实际上式4－8只是加权算术平均数的另一种表现形式，即

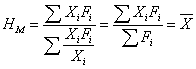，式4－9

所以，调和平均数实际上是算术平均数的一种变形，二者在本质上是一致的，唯一的区别是计算时使用了不同的数据。需要注意的时，调和平均数只适合于定比数据，而对于定距数据则不宜使用。

<三> 一种特殊的均值：几何平均数

几何平均数（ Geometric mean ）也称几何均值，它是 N 个变量值乘积的 N 次方根，计算公式为：

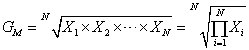，式4－9

式中， GM 为几何平均数；∏为连乘符号。几何平均数只适用于定比数据，而对于定距数据则不宜使用。