第四章 数据分布特征的测度
第一节
集中趋势的测度
三.定距和定比数据:均值
均值( Mean )也称算术平均数( Arithmetic mean ),是全部数据的算是平均。它是数据集中趋势的最主要测度量,主要适用于定距数据和定比数据,但不适用于定类数据和定序数据。均值有不同的计算形式和计算公式。
<一> 简单均值和加权均值
1.据未经分组整理的原始数据计算均值。设一组数据为 X1,X2 ,...,Xn则均值X(读作X-bar)的计算公式为
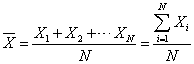 ,式4-5
,式4-5
用这个式子计算出来的均值称为简单均值( Simple mean ),其数值的大小只和变量值的大小有关。
2. 根据分组整理的数据计算均值。设原始数据被分成 K 组,各组的组中值为 X1,X2 ,...,Xn,各组变量值出现的频数分别为 F1,F2,...,Fk则均值的计算公式为:
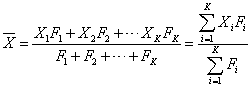 ,式4-6
,式4-6
用这个式子计算出来的均值称为加权均值( Weighted mean ),其数值的大小不仅受各组变量值( Xi )大小的影响,而且受各组变量值出现的频数即权数( Fi )的影响。如果某一组的权数较大,说明该组的数据较多,那么该组数据的大小对均值的影响就越大,反之则越小。实际上,将 4-6 式变形为下面的形式,能更清楚地看出这一点。
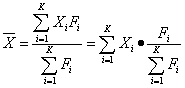 ,式4-7
,式4-7
由 式4-7可以清楚地看出,均值受各组变量值( Xi )大小和各组权数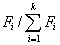 大小的影响。当我们掌握的不是各组变量值出现的频数,而是频率时,也可直接根据这个式子计算均值。
大小的影响。当我们掌握的不是各组变量值出现的频数,而是频率时,也可直接根据这个式子计算均值。
3. 均值在统计学中具有重要的地位,它是进行统计分析和统计推断的基础。首先,从统计思想上看,均值是一组数据的中心所在,是数据误差相互抵消后的必然性结果。其次,均值具有下面以下重要的数学性质,这些数学性质在实际中有着广泛的应用,同时也体现了均值的统计思想。
( 1 )各变量值与其均值的离差之和等于零,即 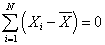
( 2 )各变量值与其均值的离差平方和最小,即 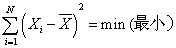
 您现在的位置 | 步进教学 | 第四章 | 第一节 | 第4页 (共6页)
您现在的位置 | 步进教学 | 第四章 | 第一节 | 第4页 (共6页) 您现在的位置 | 步进教学 | 第四章 | 第一节 | 第4页 (共6页)
您现在的位置 | 步进教学 | 第四章 | 第一节 | 第4页 (共6页)