第四章 数据分布特征的测度

    内容简介：为进一步掌握数据分布的特征和规律，进行更深入的分析，还需要找到反映数据分布特征的各个代表值。对统计数据分布的特征，可以从三个方面进行测度和描述：一是分布的集中趋势，反映各数据向其中心值靠拢或聚集的程度；二是分布的离散程度，反映各数据远离其中心值的趋势；三是分布的偏态和峰度，反映数据分布的形状。这三个方面分别反映了数据分布特征的不同侧面，本章将重点讨论这些代表值的计算方法、特点及其应用场合。

第一节 集中趋势的测度

集中趋势（ Central tendency ）是指一组数据向某一中心值靠拢的倾向，测度集中趋势也就是寻找数据一般水平的代表值和中心值。需要强调的是，低层次数据的集中趋势测度值适用于高层次的测量数据，反过来，高层次数据的集中趋势测度值并不适用于低层次的测量数据。因此，选用哪一个测度值来反映数据的集中趋势，要根据我们所掌握的数据的类型来确定。

一. 定类数据：众数

众数 (Mode) 是一组资料中出现次数量最多的变量值，因此也可以代表数据的集中趋势，用 M0表示。它主要用于测度定类数据的集中趋势，当然也适用于作为定序数据以及定距和定比数据集中趋势的测度值。

例如，在第三章例3－1 的数据中，甲城市中对住房表示不满意的户数最多，因此众数为“不满意”这一类别，即 M0＝不满意；乙城市中对住房表示不满意的户数最多，因此众数也为“不满意”这一类别，即M0＝不满意。

对于定距和定比数据同样也可以计算众数。当数据未分组是，出现次数最多的变量值即为众数；当数据经过分组整理后，众数的数值与其相邻两组的频数分布有一定的关系，

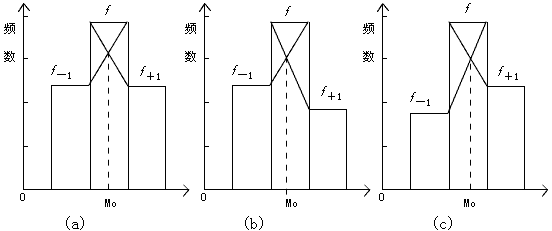图 4 － 1