第四章 数据分布特征的测度

第一节 集中趋势的测度

二.定序数据：中位数（ Median ）

中位数是一组数据按从小到大排序后，处于中间位置上的变量值，用 Me 表示。显然，中位数将全部数据等分成两部分，每部分包含 50 ％的数据，一部分数据比中位数大，另一部分则比中位数小。中位数是一个位置代表值，它主要用于测度定序数据的集中趋势，当然也适用于定距和定比数据的集中趋势，但不适用于定类数据。

根据未分组数据计算中位数时，要先对数据进行排序，然后确定中位数的位置，其公式为：

中位数位置＝（ N ＋ 1 ） /2 ，

式中的 N 为数据的个数，最后确定中位数的具体数值。

设一组数据为 X1,X2, ..., Xn ，按从小到大排序后为 X(1),X(2),..,X(N), 若 N 为奇数，则中位数为 X_(N＋1)/2 ；若 N 为偶数，则中位数是 X_N/2 与 X_N/2+1 的平均数。即

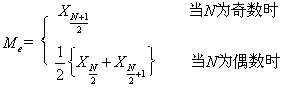，式4－2

根据分组数据四算中位数时，要先根据公式 N/2 确定中位数的位置，并确定中位数所在的组，然后采用下面的公式计算中位数的近似值：

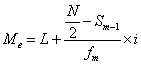，式4－3

式中N 为数据的个数（总次数）； L 为中位数所在组的下限值； S_m-1 为中位数所在组以前各组的累积频数； f_m 为中位数所在组的频数； i 为中位数所在组的组距。

计算中位数时，假定中位数所在组的频数在该组内是均匀分布的。由于中位数也是一个位置代表值，其数值的大小不受极大值和极小值的影响，因此中位数具有稳健性和耐抗性的特点。此外，中位数还具有这样一个性质，就是各变量值与中位数的离差绝对值之和最小，即

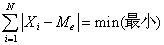，式4－4

这一性质表明，中位数和各数据的距离之和最短，这在工程设计中有一定的应用价值。

中位数的性质

１、中位数位于依序排列资料的中间位置，不易受极端值的影响，是较稳健的集中趋势测度量指标。